 |
Analiza statystyczna niewielkiej serii pomiarów bezpośrednich na przykładzie wyznaczania ładunku właściwego elektronu metodą podłużnego pola magnetycznego |
 |
Witam Wszystkich na stronie poświęconej analizie niewielkiej liczby pomiarów bezpośrednich. |
| Główną uwagę poświęcimy opracowaniu rachunku błędów uzyskanych pomiarów. Krok po kroku zostało wyjaśnione, jak doprowadzić do podania końcowego wyniku pomiaru wraz z jego dokładnością (niepewnością pomiarową). Wykorzystany przykład wyznaczania ładunku właściwego elektronu e/m ilustruje m.in. zastosowanie metody Studenta-Fischera, niezbędnej przy niewielkiej liczbie pomiarów ( zbyt małej, by stosować podejście jak dla rozkładu normalnego ). Szerzej została opisana poniżej. Zapraszam zatem do lektury :) |
| Słowo wstępne: Opis metody Studenta - Fischera |
| Przydatna pomoc: >> Tabela stałych Studenta << |
W naszym doświadczeniu do opracowania uzyskanych wyników pomiaru wykorzystamy metodę Studenta - Fischera. Spowodowane jest to tym, że nasza seria będzie składać się z niewielkiej liczby pomiarów. Wówczas prawdopodobieństwo, że odpowiednie przedziały ufności obejmą wartość rzeczywistą, jest znacznie mniejsze, niż w przypadku większej liczby pomiarów. Aby temu zapobiec i uzyskać prawdopodobieństwo takie, jak dla większej liczby pomiarów, należy odchylenie standardowe 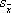 pomnożyć przez odpowiedni współczynnik Studenta t(n,p) zależny od liczby
pomiarów oraz przyjętego prawdopodobieństwa. Powstały przedział określony poniżej: |
 |
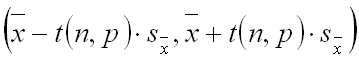| nosi nazwę przedziału ufności i zawiera w sobie wartość rzeczywistą pomiaru wraz z przyjętym prawdopodobienstwem p Powyższe prawdopodobieństwo z jakim przedział ufności obejmuje wartość rzeczywistą, nosi nazwę poziomu ufności. Najczęściej korzysta się z dwóch poziomów ufności, a mianowicie z p = 0,6827 i p = 0,9973. |
 |
 |
| fotonPK@gmail.com |