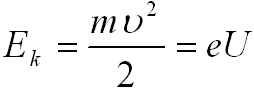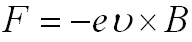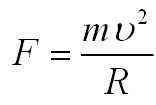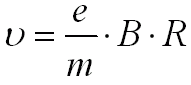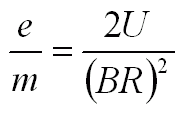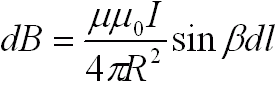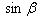| Na początek wyprowadzimy parę wzorów, niezbędnych w dalszych obliczeniach, w oparciu o konkretne przykłady.
Weżmy sobie elektron, który będzie przyspieszany różnicą potencjałów U. Wówczas pole elektryczne
nada mu energię kinetyczną:
|
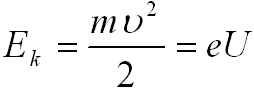
|
- v - prędkość elektronu,
- e - ładunek elementarny,
- v - masa elektronu,
|
|
Natomiast w polu magnetycznym o indukcji B siła Lorentza działająca na elektron
poruszający się z prędkością v działa siła:
|
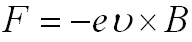
|
|
Jeżeli przyjmiemy, że pole magnetyczne jest jednorodne, wówczas torem ruchu elektronu będzie linia śrubowa
o osii równoległej do lini sił pola (Rys. 1)
|
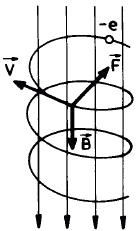
Rys. 1. Tor ruchu elektronu w jednorodnym polu magnetycznym.
|
|
W przypadku, gdy wektor prędkości elektronu jest prostopadły do wektora indukcji magnetycznej, mamy wtedy do czynienia
z ruchem po okręgu. Siła Lorentza pełni rolę siły dośrodkowej. Podczas ruchu po okręgu na elektron działa również siła dośrodkowa bezwładności:
|
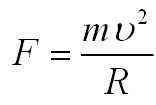 |
|
Z równości działających sił dośrodkowych otrzymujemy związek pomiędzy prędkością elektronu a promieniem okręgu R, po którym się porusza:
|
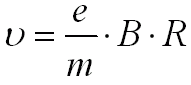
|
|
Podstawiając to wyrażenie do równania na energię kinetyczną, otrzymijemy:
|
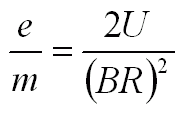
|
|
Pozostaje nam jeszcze obliczyć indukcję pola magnetycznego B. Skorzystamy tutaj z prawa Biota-Savarta:
|
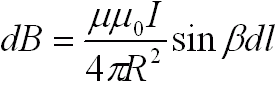
|
- db - indukcja pola magnetycznego wytwarzanego przez elementarny odcinek dl przewodnika, w którym płynie prąd I,
- R - odległość odcinka dl od punktu, w którym obliczamy indukcję pola magnetycznego,
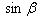 - kąt między wektorami dl i R. - kąt między wektorami dl i R.
|